Expert Choice Solutions combine collaborative team tools and proven mathematical techniques to enables your team obtain the best decision in reaching a goal. The Expert Choice process lets you:
Upon completion of an Expert Choice evaluation, you and your colleagues will have a thorough, rational, and understandable decision that is intuitively appealing and that can be communicated and justified.
.png?width=466&name=decision-process%20(1).png)
This might take the form of (a) choosing an alternative course of action, or (b) allocating resources to a combination (portfolio) of alternatives. The process is iterative and not necessarily one pass through a fixed number of steps. The process involves combining logic and intuition with data and judgment based on knowledge and experience.
Structuring is the first step in both making a choice of the 'best' (or most preferred) alternative as well as in optimally allocating resources to a combination of alternatives.
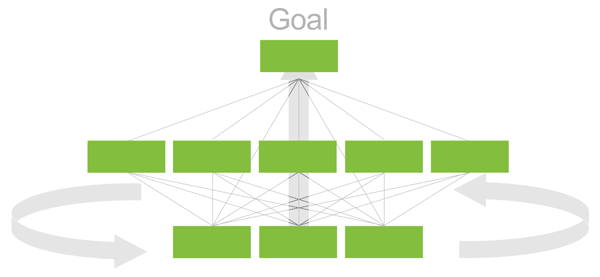

Structuring involves identifying alternative courses of action, identifying objectives (sometimes called criteria) into a hierarchy, determining which objectives each of the alternatives contribute to, and identifying participants and their roles (based on governance considerations where appropriate).
After structuring a hierarchy of objectives and identifying alternatives, priorities are derived for relative importance of the objectives as well as the relative preference of the alternatives with respect to the objectives.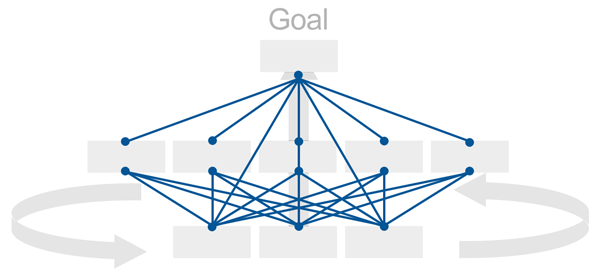
 Originally, all measurement with AHP was performed by pairwise relative comparisons of the elements in each cluster of the hierarchy, taken two elements at a time. For example, if a cluster of objectives consisted of Cost, Performance, Reliability, and Maintenance, judgments would be elicited for the relative importance of each possible pair: Cost vs. Performance, Cost vs. Reliability, Cost vs. Maintenance, Performance vs. Reliability, Performance vs. Maintenance and Reliability vs. Maintenance.
Originally, all measurement with AHP was performed by pairwise relative comparisons of the elements in each cluster of the hierarchy, taken two elements at a time. For example, if a cluster of objectives consisted of Cost, Performance, Reliability, and Maintenance, judgments would be elicited for the relative importance of each possible pair: Cost vs. Performance, Cost vs. Reliability, Cost vs. Maintenance, Performance vs. Reliability, Performance vs. Maintenance and Reliability vs. Maintenance.
While pairwise relative comparisons are used in AHP and Expert Choice to derive the priorities of the objectives in the objectives hierarchy,AHP and Expert Choice were subsequently modified to incorporate absolute as well as relative measurement for deriving priorities of the alternatives with respect to the objectives.
 All measures derived with Expert Choice possess the ratio scale levels of measure. If priorities do not possess the ratio level property, as often occurs with other decision methodologies, such as weights and scores in a spreadsheet, the results are likely to be mathematically meaningless.
All measures derived with Expert Choice possess the ratio scale levels of measure. If priorities do not possess the ratio level property, as often occurs with other decision methodologies, such as weights and scores in a spreadsheet, the results are likely to be mathematically meaningless.
Measurement can be performed by making pairwise relative comparisons, or by using absolute rating scales. Expert Choice allows for subjective as well as objective measurement. This capability makes it somewhat unique in that most mathematical models don't allow for human judgment to the extent possible with AHP and Expert Choice. Furthermore, all measures derived with Expert Choice are 'ratio level measures', an important property that avoids computations that lead to mathematically meaningless results.
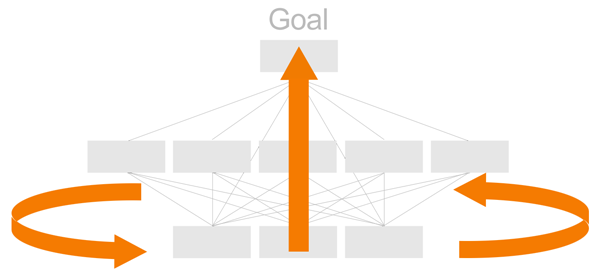
This synthesis is quite unique (as far as models go) since it includes both objective information (based on whatever hard data is available) as well as subjectivity in the form of knowledge, experience, and judgment of the participants.
The synthesis results include priorities for the competing objectives as well as overall priorities for the alternatives. Because of the structuring and measurement methods used by Expert Choice, the results are mathematically sound, unlike many traditional approaches such as using spreadsheets to rate alternatives.
But having mathematically sound results is not enough. The results must be intuitively appealing as well. The synthesis workflow step provides tools (such as sensitivity analysis and consensus measures) to allow you and your colleagues to examine the results from numerous perspectives. Using these tools, you can ask and answer questions such as "What might be wrong with this conclusion?" Why is Alternative Y not more preferable than Alternative X? If we were to increase the priority of the financial objective, why does Alternative Z become more preferable? Why might others in the organization feel that Alternative W should have a higher priority than alternative X?
The answers to one or more of these questions might signal the need for iteration. If for example, you feel that Alternative Y might be more preferable than Alternative X because of its style, and style is not one of the objectives in the model, iteration is necessary. If style is already in the model, does increasing the importance of style shift the priorities such that Alternative Y becomes more preferable than alternative X? If not, then perhaps the judgments were entered incorrectly, and iteration to re-examine the judgments is called for. If style is already in the model and the judgments are reasonable, how much would the importance of style have to be changed before the decision were reversed? If it is just a little bit, then you might reconvene those whose role it was to prioritize style and ask that they discuss their judgments and feel that they are reasonable.

Comparion Resource Aligner helps you if you are deciding on a combination of actions to take, such as a portfolio of capital investments or projects, then the allocation step is a powerful way to determine an optimal combination of actions or investments subject to constraints such as budget, personnel, space, materials, coverage, balance, and dependencies.
Using Expert Choice Comparion Resource Aligner you will be able to enter additional information pertaining to costs, risks, funding pools, dependencies and other constraints that will enable you to determine an optimal combination of alternatives under different scenarios.
The following information is an overview of the resource allocation process as it is typically applied in applications such as project portfolio management.
We won't discuss details of the Resource Aligner application here but will give an overview instead. The figure above shows the optimum combination of projects given a budget of $11 million. Projects in yellow are in the optimal portfolio. This is typically only the first 'iteration' for an optimum portfolio. Subsequent iterations will evolve as decision makers discuss dependencies, balance and coverage, musts and must nots, and other resource constraints such as specific type of personnel, building space, etc.
The Benefits column shows the relative benefits of each of the alternatives (often projects in a project portfolio application) that were derived in Expert Choice Comparion.
Costs are typically dollar costs, but can be any constraint (such as Full Time Equivalents -- FTE's) that places a limitation on selecting all of the alternatives. You can specify many different constraints from the Resource Aligner tab in addition to the 'Cost' constraint on the data grid tab. The 'Cost' constraint, however, has a special function in that it can be used to generate a 'Pareto' curve that shows different optimum portfolios (combinations of alternatives) at different maximum cost values.
Project risks (one of the three types of risk that pertain to portfolios of alternatives or projects) can be entered directly into the risk column.
The risks should be ratio scale estimates of the relative risk of the alternatives or projects. If you need to derive such estimates, you can create and evaluate an 'associated' risk model using the Risks pull down menu:
<p
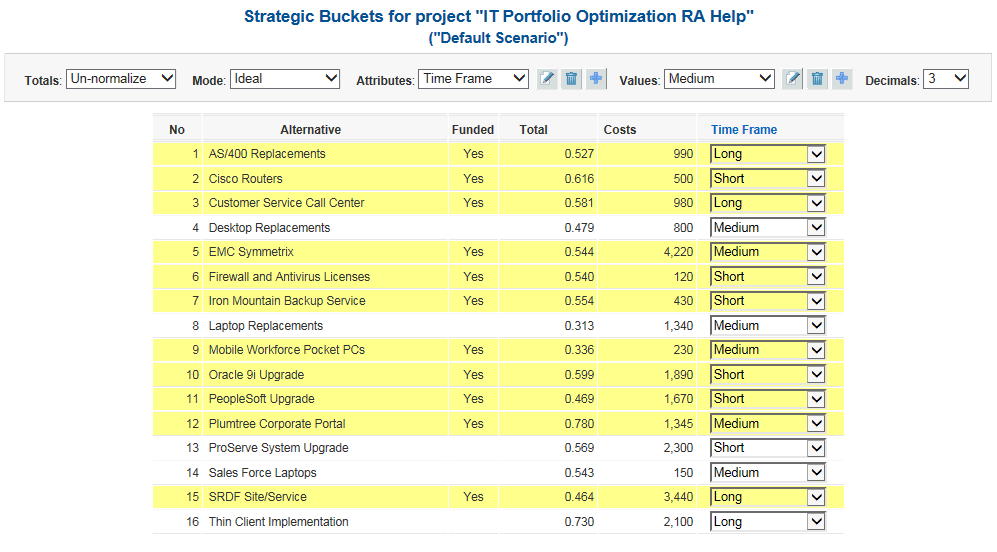
You can set up "Strategic Buckets" by designating categories for the alternatives/projects. Typical categories might include type of project, business area addressed, time-frame, level of risk, geographical region, etc.
The figure below shows the result of adding a "Time frame" attribute with Short, Medium, and Long term category items:
Benefits vs. Costs 2D Plots
The figure below shows a 2d plot of benefits vs. costs for a set of projects, color coded by the Time frame category. Some organizations that don't have access to a resource aligner optimizer might use such a plot to hand select a 'balance' of projects that tend to be in the upper left of the plot (high benefit and low cost).
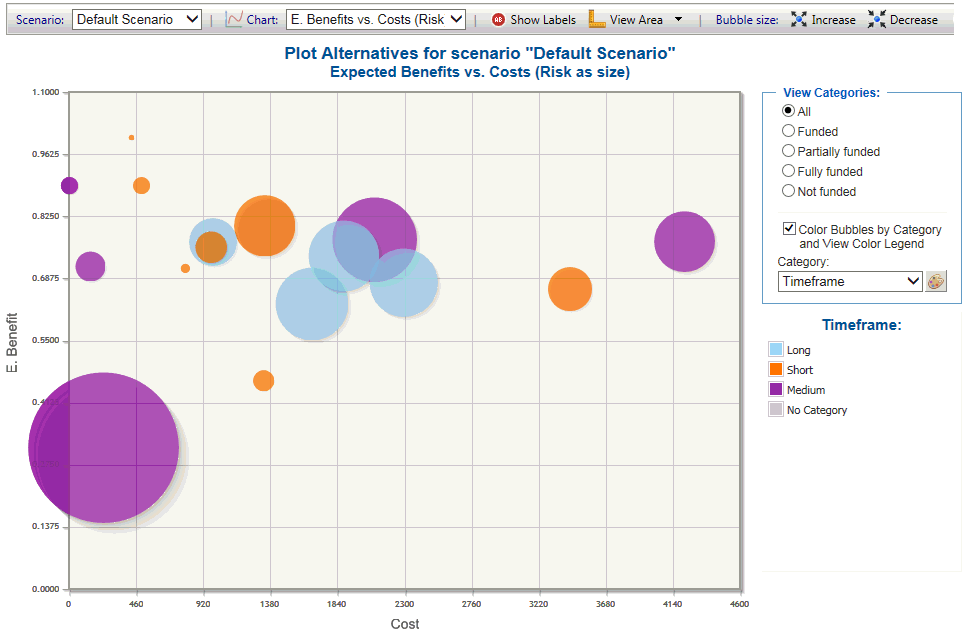
They might also try to get some 'balance and coverage' for different strategic buckets such as Time frame.
We can create a plot as above, but show only the funded projects or other plot view options:
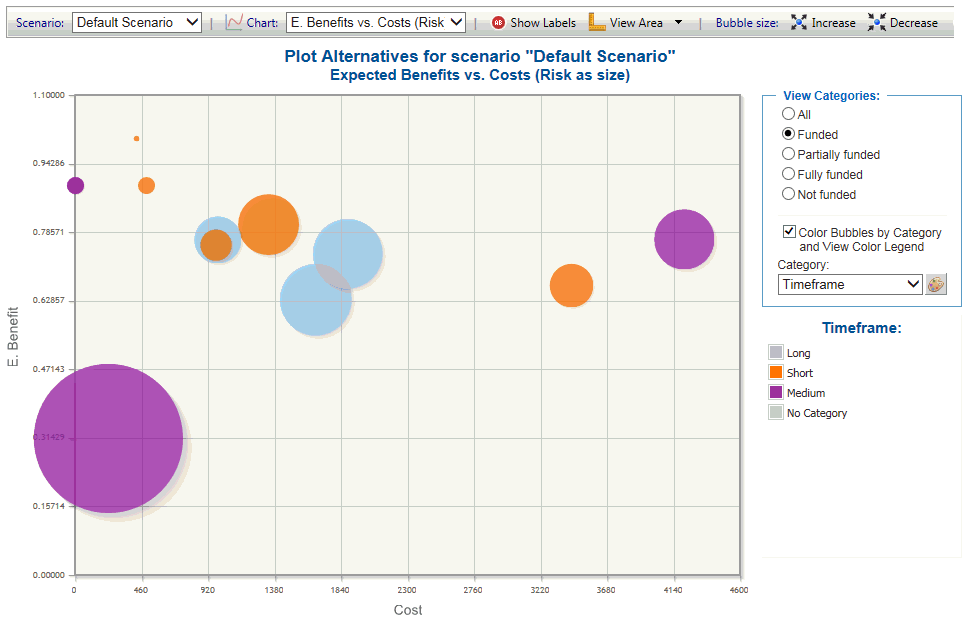
We could do this for different strategic bucket categories and look for cases where there may be an imbalance or lack of coverage. If we observe any, we could then add constraints to the resource aligner to constrain the projects in a category to some maximum or minimum number.
There are many other capabilities available so that the decision makers can easily mold the optimum portfolio to their needs and wants.
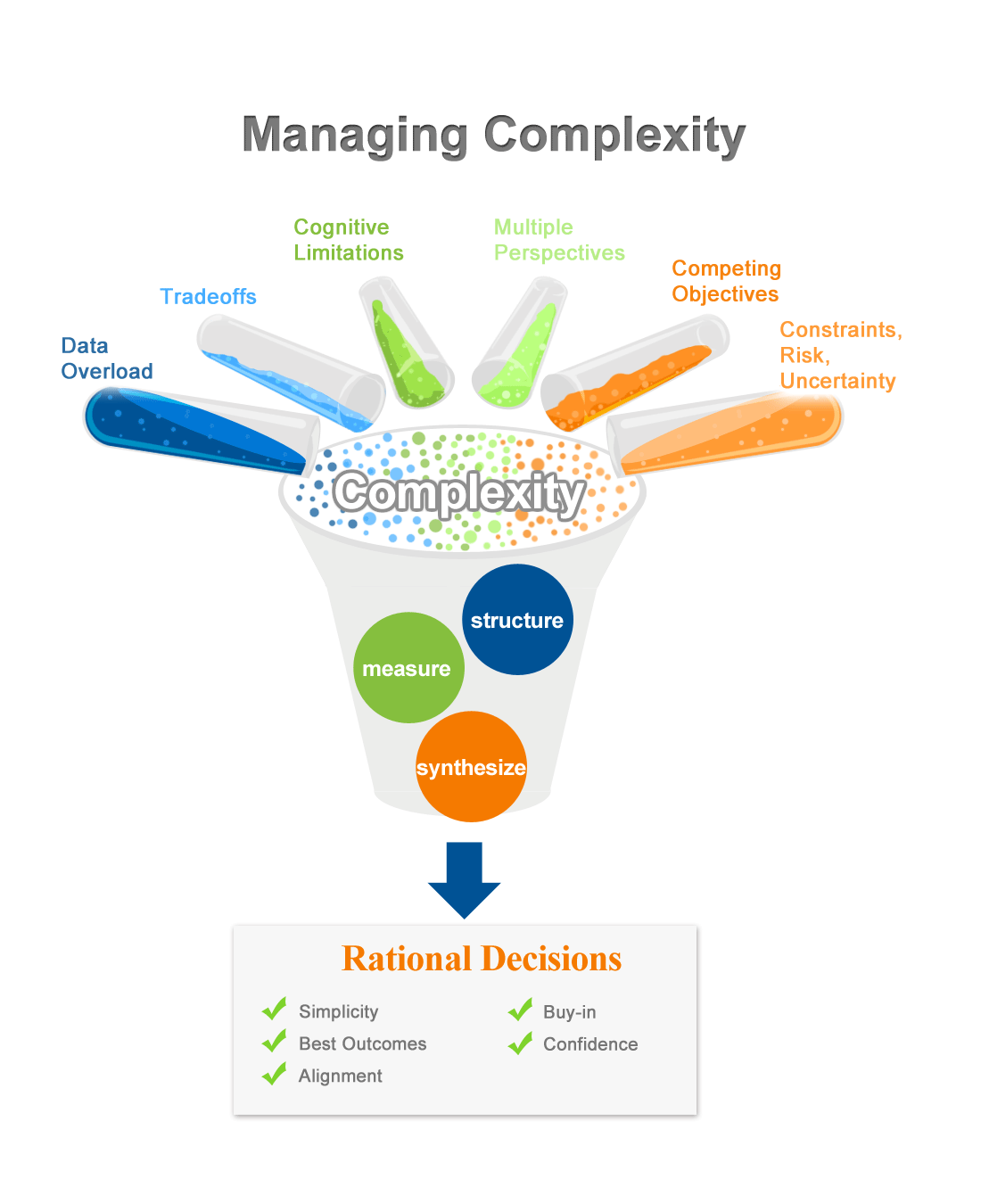
The decisions and resource allocations that Expert Choice are applied to are almost always complex, important (even crucial) and thus require iteration. One pass through a series of steps is hardly ever enough. There are many reasons for this including but not limited to:
A sensitivity analysis graph shows that the most costly alternative increases in priority as the importance of cost increases, indicating that judgments were entered incorrectly, e.g. in making a pairwise comparison, which alternative is more costly, rather than which is more preferred with respect to cost.
A performance analysis graphs shows that one alternative is best on every objective and every sub-objective! This is a sign of either a trivial decision, or more likely a sign that something was overlooked because if an alternative is best on every objective except cost, for example, it is most likely going to cost more. If this occurs, look at the pros and cons of the alternatives, especially the cons of the alternative that is best on every objective. The cons of this alternative should 'point to' objectives for which this alternative is NOT best! If you then add one or two objectives or sub-objectives based on the cons of the best alternative, you can send a link to participants to re-evaluate the project and click on 'next unassessed' to enter the few additional judgments necessary.
Perhaps the most important reason is that your intuition does not agree with the results. AHP and Expert Choice models are unlike any other economic or management models in that they can and should incorporate any and all considerations -- qualitative as well as quantitative, subjective as well as objective. With adequate iteration, the results obtained with Expert Choice will always make sense. In some cases, the iteration will change the priorities of the alternatives to match ones intuition while in other cases ones intuition will change due to insights gained from the model.
There is no fixed sequence for iteration. In some cases, it might be obvious that additional alternatives should be identified or designed.
In other cases, additional objectives added to the objectives hierarchy. Participant roles and judgments might need to be reexamined and discussed.
For either of the above cases you can return to the Structuring step at the top level workflow, or click on the link to structuring in the structuring tabby under this Iteration step which will take you there as well.
In some cases you might want to review the judgments made in the Measurement step.
You can return to the Measurement step at the top level workflow, or click on the link to Measurement in the Measurement tabby under this Iteration step which will take you there as well.
Hint: Before iterating, you might want to make a copy of the project using the Save as option found in the Home|Projects page:
Regardless of what steps might be involved in iteration, the time required for iteration should be included in planning the decision process, and never as an afterthought. If iteration is required but not performed, two important benefits of the decision process are jeopardized: The ability to justify the decision to others who might object or delay, and the ability to track the success of the decision process over time.
Reports Page Icons
The following tabbyle lists and describes the icons that display on the Reports page.
Designed to reflect the way people actually think, AHP was developed in the 1970’s by Dr. Thomas Saaty at the Wharton School of Business. Saaty joined Dr. Ernest Forman, professor of management science at George Washington University in 1983 to co-found Expert Choice. Forman adapted AHP to be able to handle complex interactions that exist alternative and objective priorities to correctly handle rank reversals. Forman also introduced algorithms to permit synchronous and asynchronous data collection from teams to perform sensitivity analyses. In the late 80's Forman expanded Expert Choice Comparion to include optimized resource allocations based on AHP derived priorities, subject to resource constraints and dependencies. Through the 90s, Forman also introduced advances to optimize across time periods, include collaborative brainstorming features, and consensus views. Recent advances include added structural capabilities, algorithms and the introduction of simulation to reflect advances made in behavioral science to accommodate identification and measurement of risk and opportunity with uncertainty. To learn more read HBR's 2006 A brief history of decision-making.
Expert Choice software engages decision makers by structuring a decision into parts, proceeding from the goal to objectives to sub-objectives down to the alternative courses of action (Comparion) and controls (Riskion) . Decision makers then use a combination of simple pairwise comparison judgments or ratio based ratings throughout the hierarchy to arrive at overall priorities for the alternatives (Comparion) or the relative risk events (Riskion). The decision problem may involve social, political, technical, and economic factors.
Expert Choice software helps people cope with the intuitive, the rational and the irrational, and with risk and uncertainty in complex settings. Expert Choice helps to:
Expert Choice is intuitive, graphically based and structured in a user-friendly fashion so as to be valuable for conceptual and analytical thinkers, novices and category experts. Because the criteria are presented in a hierarchical structure, decision makers are able to drill down to their level of expertise, and apply judgments to the objectives deemed important to achieving their goals. At the end of the process, decision makers are fully cognizant of how and why the decision was made, with results that are meaningful, easy to communicate, and actionable.
© 2026 Expert Choice. All Rights Reserved.